GEO 580 - Lecture 3
Assessing Geographic Distributions

Assessing Geographic Distributions

maps are numbers first, pictures later

maps can be descriptive AND prescriptive

from map display to map analysis map statistics or mapematics

Statistics

- typical measurement (average)

- how typical that typical is (std. deviation)

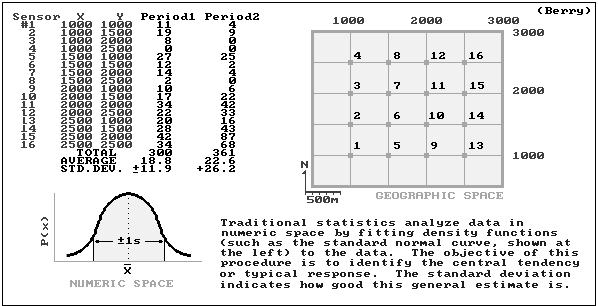
Spatial statistics - variation (std. deviation) in geographic space

- guidance as to where the typical is too low and where it is too high

What's A Wildlife Manager to Do?

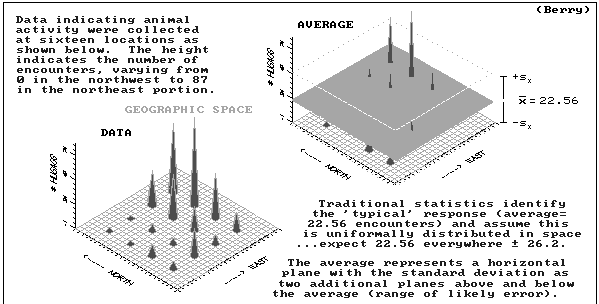
23 animals assumed everywhere?

coefficient of variation often useful
-- if std. dev. large, average is unusable
-- error flag pitfalls of applying classical statistics to spatial data

give spatial characterization to the mean (23)

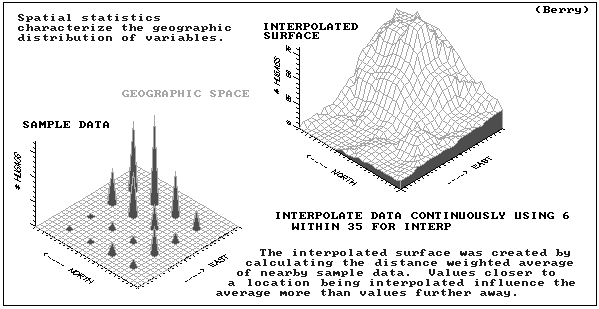
lets interpolate!

Spatial Interpolation

estimates must be determined from surrounding values

Fitting Continuous Surfaces to Data

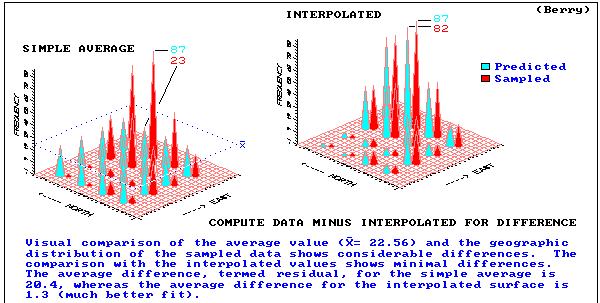
(1) FLAT plane

(2) flat but TILTED to fit data better

(3) tilted but WARPED to fit data even better

Trend Surface

point-based

approximate interpolater

- surface doesnt pass through all data points

- global trend in data, varying slowly overlain by local but rapid fluctuations

global interpolater - change in an input value affects the entire map

• surface is approximated by a polynomial

• output data structure is a polynomial function which can be used to estimate values of grid points on a raster or the value at any location

• the elevation z at any point (x,y) on the surface is given by an equation in powers of x and y
  • e.g. a linear equation (degree 1) describes a tilted plane surface:

    z = a + bx + cy

  • e.g. a quadratic equation (degree 2) describes a simple hill or valley:

    z = a + bx + cy + dx² + exy + fy²

• in general, any cross-section of a surface of degree n can have at most n-1 alternating maxima and minima
  • e.g. a cubic surface can have one maximum and one minimum in any cross-section
  • equation for the cubic surface:

    z = a + bx + cy + dx² + exy + fy² + gx³ + hx²y + ixy² + jy³

• a trend surface is a global interpolator
  • assumes the general trend of the surface is independent of random errors found at each sampled point

• computing load is relatively light

• problems
  • statistical assumptions of the model are rarely met in practice
  • edge effects may be severe
  • a polynomial model produces a rounded surface
    • this is rarely the case in many human and physical applications
• available in a great many mapping packages

z = a + bx + cy

tilted but WARPED plane to fit data

- surface is approximated by quadratic equation (polynomial degree 2)

z = a + bx + cy + dx² + exy + fy²

On to Windows (not Microsoft's)

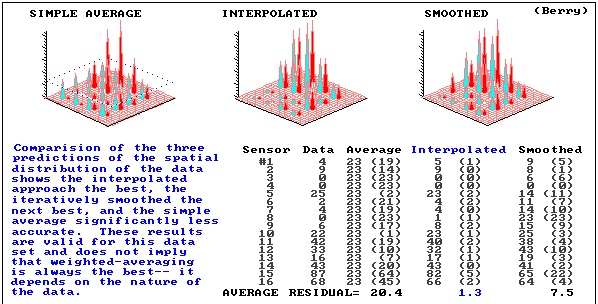
results extend non-spatial concept of central tendency

WHERE might you find unusual responses?

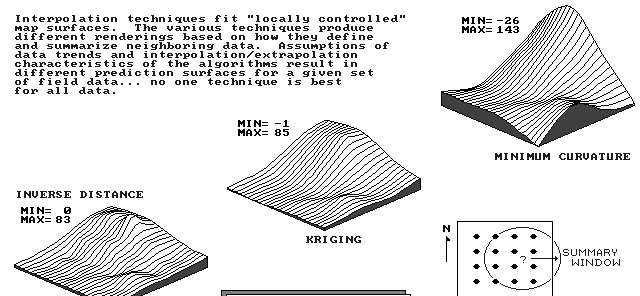
generates estimates based existing data in the region

region = roving window

- moves about study area
- summarizes data it encounters
- reach (search radius)
- number of samples
- direction

Minimum Curvature Splines

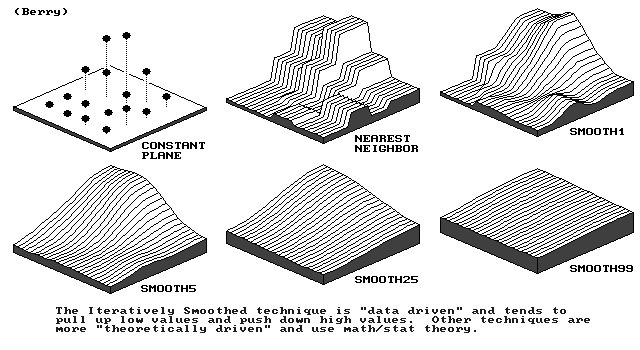
(no roving window used in nearest neighbor)

Inverse Distance Weighted

approximate interpolator

• estimates are averages of the values at n known points:

  z = Summation wi * zi / Summation wi

  where w is some function of distance, such as:

  w = 1/d^k

  w = e^-kd

• an almost infinite variety of algorithms may be used, variations include:
  • the nature of the distance function
  • varying the number of points used
  • the direction from which they are selected

• is the most widely used method

• objections to this method arise from the fact that the range of interpolated values is limited by the range of the data
  • no interpolated value will be outside the observed range of z values

independent random samples
- good for data with no regional trend

Kriging

• developed by Georges Matheron, as the "theory of regionalized variables", and D.G. Krige as an optimal method of interpolation for use in the mining industry

• the basis of this technique is the rate at which the variance between points changes over space
  • this is expressed in the variogram which shows how the average difference between values at points changes with distance between points

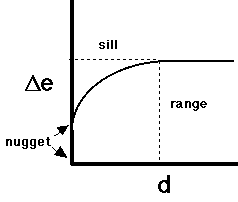
• delta-e (vertical axis) is E(zi - zj)², i.e. "expectation" of the difference
  • i.e. the average difference in elevation of any two points distance d apart
• d (horizontal axis) is distance between i and j

• most variograms show behavior like the diagram
  • the upper limit (asymptote) of delta-e is called the sill
  • the distance at which this limit is reached is called the range
  • the intersection with the y axis is called the nugget
  • a non-zero nugget indicates that repeated measurements at the same point yield different values

• in developing the variogram it is necessary to make some assumptions about the nature of the observed variation on the surface:
  • simple Kriging assumes that the surface has a constant mean, no underlying trend and that all variation is statistical

  • universal Kriging assumes that there is a deterministic trend in the surface that underlies the statistical variation

• in either case, once trends have been accounted for (or assumed not to exist), all other variation is assumed to be a function of distance

• the input data for Kriging is usually an irregularly spaced sample of points

• to compute a variogram we need to determine how variance increases with distance

• begin by dividing the range of distance into a set of discrete intervals, e.g. 10 intervals between distance 0 and the maximum distance in the study area

• for every pair of points, compute distance and the squared difference in z values

• assign each pair to one of the distance ranges, and accumulate total variance in each range

• after every pair has been used (or a sample of pairs in a large dataset) compute the average variance in each distance range

• plot this value at the midpoint distance of each range

• once the variogram has been developed, it is used to estimate distance weights for interpolation
  • interpolated values are the sum of the weighted values of some number of known points where weights depend on the distance between the interpolated and known points

• weights are selected so that the estimates are:
  • unbiased (if used repeatedly, Kriging would give the correct result on average)
  • minimum variance (variation between repeated estimates is minimum

• problems with this method:
  • when the number of data points is large this technique is computationally very intensive
  • the estimation of the variogram is not simple, no one technique is best
  • since there are several crucial assumptions that must be made about the statistical nature of the variation, results from this technique can never be absolute

• simple Kriging routines are available in the Surface II package (Kansas Geological Survey) and Surfer (Golden Software), and in the GEOEAS package for the PC developed by the US Environmental Protection Agency

Not Discussed in Class: Fourier Series

• approximates the surface by overlaying a series of sine and cosine waves

• a global interpolator
  • computing load is moderate

• output data structure is the Fourier series which can be used to estimate grid values for a raster or at any point

• best for data sets which exhibit marked periodicity, such as ocean waves

• rarely incorporated in computing packages

Arc/INFO Interpolation Methods

Spatial Interpolation & GIS

to provide contours

to calculate some property of a surface at a given point

model all the REAL intricacies of a surface

highlight general spatial trend of data for decision-making

A GIS Perspective on Interpolation

• we've looked at point interpolation which tries to estimate a continuous surface
  • in a point case, the surface is estimated at specific sample points
  • in the case of areal interpolation, a surface is estimated from counts within polygons (e.g., population density surface derived from total population counts in each reporting zone

• when is it impossible to conceive of a continuous? surface??
  • how about if points represent cities with attributes of city population
    • e.g., if city A has a population of 1 million and city B 100 km away has a population of 2 million, there is no reason to believe in the existence of a city half way between A and B with population of 1.5 million
  • in this case, the variable population exists only at the points, not as a continuous surface
  • in other cases the variable might exist only along lines e.g. traffic density on a street network

• the above is an example of when we must distinguish between the layer and object views of the world
  • a continuous surface of elevations is a layer view of the world - there is one value of elevation at an infinite number of possible places in the space
  • the point map of cities is an object view of the world - the space in between points is empty, and has no value of the population variable
  • the street network is an object view of the world - the world is empty except where there are streets - only along streets is traffic density defined

• spatial interpolation implies a layer view of the world, and it requires special techniques as we've discussed to apply it to objects such as point estimates of animal population or cities

Spatial Interpolation Algorithms in GIS

• a good GIS should include a range of spatial interpolation routines so that the user can choose the most appropriate method for the data and the task

• ideally, these routines should provide a natural language interface which would lead the user through an appropriate series of questions about the intentions, goals and aims of the user and about the nature of the data

• a number of prototype expert systems for guiding the choice of a spatial interpolation algorithm have been developed

• these may be written in the form of:
  • an expert system shell (Waters, 1988)
  • in one of the artificial intelligence languages such as Prolog or LISP (see Dutton-Marion, 1988)
  • or in a high level language such as Pascal (Maslyn, 1987)

• if computer contouring and surface generation techniques are to be incorporated successfully into GIS, they must be easy to use and effective
  • "easy to use" implies that those without a detailed knowledge of the mathematical and statistical characteristics of the procedure should be able to choose the correct technique for displaying a particular data set for a particular purpose
    • note: statisticians argue that this is not an ideal goal as people may use techniques without a proper understanding of the underlying assumptions

  • "effective" means that these techniques should be informative, highlighting the essential nature of the data and/or surface and serving the purpose of the researcher/analyst
    • the researcher's measure of success will be largely subjective and visual - does the result look right?

• the purpose of the interpolation may vary from an attempt to model all the "real" intricacies of the surface to simply trying to highlight the general, spatial trend of the data in order to aid in the decision-making process

Some References

Burrough, P.A., 1986. Principles of Geographical Information Systems for land Resources Assessment, Clarendon, Oxford. See Chapter 8.

Lam, N., 1983. "Spatial Interpolation Methods: A Review," The American Cartographer 10(2):129-149.

Maslyn, R.M., 1987. "Gridding Advisor: An Expert System for Selecting Gridding Algorithms," Geobyte 2(4):42-43.

http://dusk.geo.orst.edu/buffgis/buff03.html

Return to GEO 580 Lectures