
although vast majority of GISs currently work only in 2 dimensions, across the plane . . .
certain applications require the addition of other dimensions, namely elevation/depth or time
engineering design of mines, quarries, dams, reservoirs, etc.
geological/geophysical exploration
scientific explanation of 3D processes such as ocean currents or lava flows
data driven - may not necessarily know what you will find in 3D
so the structure of the representation may enhance types of analyses that can be performed
vertical dimension combined with temporal query = 4-D
most common way of doing 3D in commercial GIS packages
z value (normally elevation) is recorded as an attribute for each data point (x,y)
z values can be used in a perspective plot to create the appearance of 3 dimensions
system can accept only 1 z value for any surface at a given location
attractive way of displaying topography and other continuous surfaces from DEMs or TINs
perspective plots computed from any viewpoint
additional layers "draped" over the surface using color
"artist's impressions" - convert classes (e.g., land cover) to simulated trees, etc.
store data in structures that actually reference locations in 3D space (x,y,z)
here z is not an attribute but an element of the location of the point
data can be recorded at several points with equal x and y coordinates, e.g.,
soundings in the ocean or atmosphere, geologic logs of wells
objects are defined as polyhedra bounded by planes or faces
each object can be represented by a number of faces, edges, points
TIN is a 2.5 D type of B-rep, constrained to be single-valued (i.e. one value of z for every x,y)

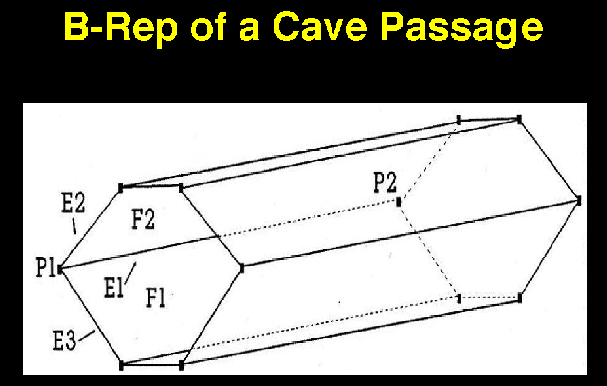
requires a powerful user-interface to construct combinatorially-complex objects
each part of the B-rep (planes, edges, points) must be carefully and consistently
defined for each application in order to maintain validity
performance degrades rapidly with high geometric complexity
algorithms for 3D spatial analysis simpler, more efficient, if data in a volumetric form
volume is divided into cubes or voxels
usually produced by converting from B-reps (similar to converting vectors to rasters in 2D)
properties like mass, volume and surface area are quickly computed as
Boolean operations [on (full) / off (empty)] or voxel counts

these 3D representations are relatively new, so there is little collective experience on how to implement them in the earth sciences and engineering not too many truly 3D GIS packages on the market
2- or 2.5D GIS linked to 3D modeling package
HOWEVER, needs of these fields different from earth sciences
time dependent (need to track moving objects between one 3D image and the next)
some earth science applications do not require this, some do
time dependence adds a third dimension to spatial data, just as the vertical dimension does
or may be added to 3 spatial dimensions to give 4D
computer science deals with time dependence of records in databases e.g., records may be valid only for limited times
geographical cases are more complex - objects may have limited existence, but
may also move, change shape, and change attributes
once again, set of database models for time dependent data have not been fully developed
very few temporal GISs on the market
shapes of objects change through time
define a limited number of time "slices"
store the objects at each slice
objects may coalesce or split from one time slice to the next
e.g. kelp beds off the Oregon coast
or use a 3D space with the vertical dimension as time, populated by 3D objects (4D)
attributes of objects change through time
define a limited number of time "slices"
store the attributes as separate tables for each time slice
if attributes are needed between time slices, interpolate
boundaries between objects change through time
boundaries may turn on and off rather than move
the system stores all boundary lines which ever existed
then reconstructs objects from the boundaries at any given time
objects at each time slice, but unrelated from one time to another - layers
objects at each time slice, related or tracked from one time to another -
related layers
migration studies
objects defined continuously in the time dimension - 3D objects
individual space-time travel behavior
Bouille, F. 1976. "A Model of Scientific Data Bank and Its Applications to Geological Data," Computers and Geosciences 2: 279-291.
Carter, J.R. 1988. "Digital Representations of Topographic Surfaces: An Overview," in American Congress on Surveying and Mapping and American Society for Photogrammetry and Remote Sensing, Technical Papers 5:54-60.
Ganter, J.H. 1989. "Comparison of Representations for Complex Earth Volumes," Auto-Carto 9: Proceedings of the Ninth International Symposium on Computer-Assisted Cartography, Baltimore, MD.
Hagerstrand, T., 1970. "What about people in Regional Science?" Papers, Regional Science Association 24:7-21. Discusses the concept of space-time prisms in human spatial behavior.
Kavouras, M. and S. Masry, 1987. "An Information System for Geosciences: Design Considerations," Auto-Carto 8: Proceedings of the Eighth International Symposium on Computer-Assisted Cartography, ASPRS/ACSM, Falls Church, VA, pp. 282-291.
Langran, G., 1989. "A review of temporal database research and its use in GIS applications," International Journal of Geographical Information Systems 3(3):215-32. Can research on time dependence in databases help in representing the effects of time in GIS data?
Langran, G. and N.R. Chrisman, 1988. "A framework for temporal geographic information," Cartographica 25(3):1- 14. Discusses models for representing temporal change in GIS.
Mark, D.M. and J.A. Cebrian, 1986. "Oct-trees: A Useful Data- Structure for the Processing of Topographic and Sub- Surface Data," ACSM/ASPRS Technical Papers 1:104-113.
Raper, Jonathan. Three Dimensional Applications in GIS, Taylor and Francis, New York. A collection of papers on the developing technology of 3D GIS.
Requicha, A.A.G. 1980. "Representations for Rigid Solids: Theory, Methods and Systems," ACM Computing Surveys 12:437-464.
Turner, A.K. 1997. "What's the Difference Among 2-D, 2.5D, 3-D, and 4-D?" GIS World 10(3): 54.