[ home port | lectures | labs | discussion | announcements | surf | email prof. ]

Things to Get Out of This Lab:

• An understanding of the two fundamental properties of sea water: density and heat capacity
• Recognition of the importance of these properties in the ocean environment and in climate
• Trying your hand at scientific data collection and interpretation

Materials: Calculator, ruler, and Invitation to Oceanography textbook

Introduction

To look at the ocean is to see a vast expanse of liquid that seems to be the same everywhere. It takes the sophisticated technology of shipboard oceanographic instrumentation and space-borne satellites to tell us that the water in the oceans is quite different from place to place, particularly in terms of temperature, chemistry, and rate of evaporation. These important differences play a role in determining the circulation patterns of the oceans, which in turn affect the distribution of marine life. Also, the movement of sea water is important in controlling greenhouse gases and the temperature of the Earth's atmosphere. You will learn more about this in Lab 5. But first, here in Lab 4 you will first review the two properties of sea water that are extremely important to ocean circulation and climate: density and heat capacity.

Density

The density of a substance relative to the substances around it controls whether it will sink or float. For example, when fudge syrup is added to milk, it sinks to the bottom of the glass. This is because the fudge syrup is denser than the milk: its mass-to-volume ratio is higher than the mass-to-volume ratio of milk. The separation of the substances of differing densities is called stratification. In the ocean (and other bodies of water), we observe a stratification of water masses of differing densities, similar to the stratification of syrup and milk in a glass (note that a water mass is a volume or body of water with similar chemical and/or physical properties, usually identified by temperature and salinity).

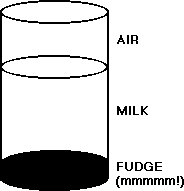
Density in the ocean is controlled primarily by differences in temperature and salinity. These properties drive what is known as the thermohaline circulation of water in the ocean. Thermo- refers to the temperature component of density, whereas -haline refers to the salinity component.

Below is a summary of the effects of temperature and salinity on density. You may find it helpful to review Chapter 4 on "Properties of Sea Water" in your text.

Review of Density

Density (D or [rho]) is a property of all kinds and states of matter: solids, liquids, and gases. It is defined as the ratio of mass to volume. The simple equation of density is:

SOLUTION:

Step 1: D or density is the unknown. M or mass = 900 g. V or volume = 1 L

Isolate the unknown.

D = M / V D (g/cm³) = 900 g / 1 L

Step 2: Check the units. We must convert liters to cm³.

1 L = 1000 ml = 10³ ml = 10³ cm³ or 1000 cm³

Step 3: Substitute values with correct units into the original equation and solve.

D = 900 g / 1000 cm³ = 0.9 g/cm³

The units of density depend directly on the units of mass and volume. In the metric system, density is often measured in g/cm³. The density of pure water at 4° C is 1.00 g/cm³. The density of sea water in the open ocean ranges between 1.02 and 1.04 g/cm³. Since variations in the density of water masses occur in and beyond the second decimal place, it is convenient in oceanography to use what is known as the "sigma" notation:

SOLUTION: [sigma]_T = (1.025 g/cm³ - 1) * 1000 = 25

The density of sea water is primarily controlled by two properties: temperature and salinity. Changes in temperature affect density by changing the volume a given mass of water occupies. Changes in salinity affect density by changing the mass a given volume of water occupies. The figure on the next page illustrates the affects of temperature and salinity on density.

Temperature's Effect on Density

There is an inverse relationship between temperature and density:

Increasing the temperature causes substances to expand and become less dense. This is because as a substance acquires heat (a source of energy), its molecules vibrate more and "demand" more space. However, the addition of heat does not change the mass of the substance. An increase in volume without an increase in mass decreases the mass-to-volume ratio and density decreases. Decreasing the temperature causes the opposite effect. As a substance loses heat, its molecules have less energy to move around and therefore "require" less space. Again, a loss of heat does not change the mass of the substance. A decrease in volume without a decrease in mass increases the mass-to-volume ratio. Therefore, decreasing the temperature generally causes an increase in density.

The maximum density of pure water occurs at 4° C. As pure water cools below 4° C, it becomes less dense until it freezes at 0° C. This is because as liquid water freezes, hydrogen bonds form an open structure of ice. Because the structure of ice is more open than liquid water It occupies a greater volume and is less dense. This is why ice floats on top of water.

Salinity's Effect on Density

There is a direct relationship between salinity and density:

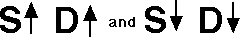
In order to understand this relationship, it is important to define salinity. A simple definition of salinity is the total amount of dissolved salts per unit of water. The salinity of sea water is commonly measured in g/kg or o/oo (o/oo is read as "parts per thousand" or "per mil). Recall that 1000 g = 1 kg so g/kg is the same as g/1000 g. For example, the mean (average) salinity of the oceans is 34.7 o/oo. Salinity may be expressed by the simple equation:

SOLUTION:

Step 1: Grams of salt is the unknown quantity.

Mass of sea water = 4 kg. S or salinity = 35 o/oo

Isolate the unknown.

S = g of salt / kg of sea water g of salt = (S)(kg of sea water)

Step 2: Check the units. We must convert o/oo to g/kg.

1 o/oo = 1 g/kg, therefore 35 o/oo = 35 g/kg

Step 3: Substitute values with correct units into the original equation and solve.

g of salt = (S)(kg of sea water) = (35 g/kg)(4 kg) = 140 g of salt

Salinity is a function of the amount of dissolved salts in a unit of water. As salinity increases, the total mass of water (pure water + the dissolved salts) in a given volume, density increases. Therefore, an increase in salinity increases density. The table below lists the six most abundant salts in sea water.

Ion = % Abundance

Chloride (Cl^-) = 55.07

Sodium (Na⁺) = 30.62

Sulfate (SO₄^-2) = 7.72

Magnesium (Mg⁺²) = 3.68

Calcium (Ca⁺²) = 1.17

Potassium (K⁺) = 1.10

Heat Capacity

Heat capacity is defined as the amount of heat (calories) required to change the temperature of 1 g of a substance 1° C. It can be thought of as the ability of a substance to absorb or release heat energy without a change in temperature. Substances with high heat capacities absorb more heat before changing temperature than substances with low heat capacities. If you have ever heated water in a metal pot on a stove or campfire, you may have noticed that the metal pot heated up much faster than the water. This is because metal has a lower heat capacity than water. A substance with a high heat capacity can absorb and release more heat per degree temperature change than a substance with a low heat capacity. A substance with a low heat capacity can absorb and release less heat per degree temperature change than a substance with a high heat capacity.

Heat capacity can be expressed by a simple equation which is really just a statement of its definition:

H_c = C / M*[Delta]T

where H_c = heat capacity in cal/g° C

C = heat required in cal

M = mass in g

[Delta]T = (T₂ - T₁) = change in temperature in °C

EXAMPLE: 50 calories of heat raises the temperature of 25 g of water 22° C to 24° C. What is the heat capacity of water?

SOLUTION:

Step 1: H_c is the unknown quantity.

Mass = 25 g. [Delta]T = (T₂ - T₁) = 24 - 22° C = 2° C C = 50 cal

Isolate the unknown.

H_c = C / M* [Delta]T

Step 2: Check the units. No conversions are necessary.

Step 3: Substitute values with correct units into the original equation and solve.

H_c = C / M* [Delta]T H_c = 50 cal / (25 g)(2° C) = 1 cal/g° C

As the above example demonstrates, the heat capacity of water is

1 cal/g° C. Water has a higher heat capacity than most substances. Once again, the reason for this is the hydrogen bonding between water molecules.

Temperature is a measure of the motion of molecules. As we reviewed earlier, as the temperature of a substance increases so does the motion of its molecules. However, because of the hydrogen bonds in water it takes a lot of energy to set water molecules into motion. Therefore, the temperature of water rises more slowly than other substances.

Lab 4 Activities

1. The list below shows the densities of substances with which you are familiar. If you were to pour these substances into a cylindrical beaker, what would their stratification be? Write down the names of the substances in the order of your predicted stratification level with 1 being lightest and 4 being heaviest.

SUBSTANCE DENSITY (g/cm³)

Alcohol 0.79

Copper 8.90

Ice (fresh water) 0.92

Sea water 1.027

2. Use the equation for density, D = M / V, to solve the following problems.

What is the mass of 5 L of pure water ([rho] = 1.00)?

What is the mass of 5 L of sea water ([rho] = 1.027)?

3. If the salinity of 5 L of sea water ([rho] = 1.027) is 34 o/oo, how many grams of salt would it contain? (HINT: Use the mass of sea water calculated in the problem above and the equation for salinity given in the Introduction).

4. What is the most abundant ion in sea water? Is it an anion or a cation?

5. How much heat would be required to raise the temperature of 0.05 g of pure water from 20° C to 26° C? Do you think it would take more, less, or the same number of calories to raise the temperature from 95° C to 101° C? Why??

Last update: April 24, 2000
http://dusk.geo.orst.edu/oceans/lab4.html
Dawn Wright & Bob Duncan © 1999