Faulting and Magmatism at Mid-Ocean Ridges
Geophysical Monograph 106
edited by R. Buck, P. Delaney, J.A. Karson, and Y. Lagabrielle
pages 137-151, 1998.
The article below is slightly longer than the final published version.
Faulting and Magmatism at Mid-Ocean Ridges
Geophysical Monograph 106
edited by R. Buck, P. Delaney, J.A. Karson, and Y. Lagabrielle
pages 137-151, 1998.
The article below is slightly longer than the final published version.
Abstract. Fissures control the gross permeability of ocean crust, providing critical pathways for hydrothermal fluids and magma and lending important clues to the cycling of volcanic and hydrothermal processes and the spatial and temporal stability of ridge segments. And yet due to limitations in mapping technology that existed until the late 1980s, the critically important parameters of fissure abundance, spacing, length, width, and depth have rarely been reported anywhere on the seafloor, with the exception of the fast-spreading EPR. However, with the increasing availability of high resolution mapping tools, research agendas at various international workshops (e.g., Purdy and Fryer [1990], Dziewonski and Lancelot [1995], and Mottl et al. [1996]) are now citing the determination of these parameters as a high priority for morphotectonic studies of the mid-ocean ridge that seek to more fully understand the nature of extensional failure of the ocean crust. This chapter reviews the fundamentals of fissure formation and development, as well as the only known studies to have focussed specifically on fissuring at mid-ocean ridges. New fissure data are presented from work in progress on the southern East Pacific Rise at 17-18° S. Also discussed are the distinctions between tectonic and eruptive fissuring, the implications of fissures changing into faults within the neovolcanic zone, and the use of fissures for mapping out fourth-order ridge segment boundaries and assessing the cycling of magmatic and hydrothermal processes therein. The chapter concludes by posing research questions to guide future studies of fissuring in the neovolcanic zone, as well as faulting and eruption on the mid-ocean ridge crest and flanks.
Introduction
Fissures (on a "micro-scale" of 10s of meters along-strike) and faults (on a "macro-scale" of kilometers to 10s of kilometers) provide essential pathways into the upper oceanic crust through which magma and hydrothermal fluids may migrate (faults may even be primary conduits for fluid flow deep into the crust). The nature and distribution of crustal cracking provide insights into the spatial and temporal stability of mid-ocean ridge (MOR) segment and have important implications for magmatic and hydrothermal venting along the MOR crest, as well as hydrothermal circulation on- and off-axis. Crustal cracking on the order of 10's to 100's of meters in length controls the gross permeability of the crust and, ultimately, fluid flux pathways, alteration of associated igneous rock, and the physical properties of ocean crust. A fundamental question to be considered is the role of fissuring (tensile failure) versus faulting (shear failure). Fault populations on the MOR have been the subject of considerable study within the past few years (e.g., Edwards et al. [ 1991], Carbotte and Macdonald [1992 and 1994], Cowie et al. [1994], Macdonald et al. [1996], van Wyk de Vries and Merle [1996]). Similarly, in connection to faulting and magmatism on the MOR, much attention has been given to the study of subsurface dikes (i.e., magma-filled cracks; see ). However, in order to fully understand the nature of mechanical failure in an extensional environment, one must also consider the location, distribution, and geometry of fissures. In the past this has been difficult on the MOR because of the lack of good quality data at the "micro-scale." Crane [1987] was the first to tabulate fissure abundance and length along the axial zone of the MOR (using the side-looking sonars of the deep-towed Sea MARC I with selectable swath widths of 1.5, 3, and 6 km over the EPR at 10° 35' to 13䓊'N). No further studies focusing primarily on fissures were performed on any part of the MOR until the 1989 Argo I survey of the EPR at 9° 12' - 54'N provided unprecedented coverage of the axial zone (up to 80% visual coverage with a 10-16 m swath and 90% sonar coverage with a 300 m swath) [Haymon et al., 1991]. This finally provided a data set that was of sufficient density, continuity, and geographical precision to meaningfully map and analyze fissure distributions at a fine-scale [Wright et al., 1995a], as well as hydrothermal vents, lava flows, and biological communities [Haymon et al., 1991]. Indeed, given the near-bottom mapping technology, fissures offer several advantages in the field over faults: (1) large numbers may be present within a small area; (2) they are likely to be confined to a single flow morphology or lithology; and (3) they are commonly well-exposed over their entire length. This chapter reviews current ideas on fissure formation and distribution, primarily on the fast-spreading East Pacific Rise (EPR) where most of the existing data have been gathered, and discusses the important implications of ridge-crest fissuring for axial faulting, magmatism, segmentation, and the cycling of tectonic, magmatic, and hydrothermal processes.
Fissure Formation and Distribution
Background from Fracture Mechanics
For the MOR environment a fissure is here defined as an open, Mode I tension crack initiating at the surface (Figure 1). Unlike a dike, which is modeled by Rubin [this volume] as a pressurized, static, magma-filled crack in an elastic solid, a fissure is not filled with magma, but may serve as an important conduit for upwardly-propagating magma and hydrothermal fluids. This may be possible if the fissure is tectonic in origin and intersecting a horizontal lava tube or interconnected voids in the uppermost (~0-50 m) of the seafloor. Haymon et al. [1993], Perfit et al. [1993], and Goldstein et al. [1994] have documented the existence of such lava tubes and voids at the EPR, 9° N. A distinction that I will return to later in more detail is that of tectonic fissures (formed near the axis because the lithosphere is stretched as it accelerates from zero to full spreading velocity) from eruptive fissures (assocated with dikes propagating to the vicinity of the surface). Detailed discussion of the mechanics of fissure formation in volcanic environments are available only from studies on Iceland, Hawaii, and Afar (e.g., Pollard et al. [1983], Rubin and Pollard [1987], Gudmundsson and B\212ckstr\232m [1991], and Hayward and Ebinger [1996]), where quantitative field measurements and resulting theoretical models have allowed for a more thorough treatment of the problem than attempts on the seafloor (which are not unlike mapping in a dark football stadium with a flashlight [Gregg, 1997]). The Iceland, Hawaii, and Afar results are directly applicable to the MOR environment because the same mechanical processes are at work. The following is a brief review of the mechanics of fissure formation in volcanic rift zones. For a thorough introduction to fracture mechanics see Jaeger and Cook [1979] or Anderson [1995]; for applications to dike propagation see Rubin [this volume].
If [sigma]1 < -3[sigma]3, then [sigma]3 = -[Tau]0
If [sigma]1 > -3[sigma]3, then ([sigma]1 - [sigma]3)2 = 8[Tau]0([sigma]1 + [sigma]3)
This first formula applies to the tensile regime whereas formula (2) applies to compression. When considering the formation and development of fissures on the MOR several mechanical factors need to be taken into account, the most important being elastic moduli, tensile stress, and tensile strength of the host rock.
Elastic Moduli
For the complete specification of a linear elastic material, any two of the elastic moduli ([lambda],
Lamé's constant; G, the shear modulus (rigidity); [nu], Poisson's ratio; E, Young's modulus; or K, the bulk modulus) must be known [Jaeger and Cook, 1979]. For MOR fracture mechanics models Poisson's ratio is used either with Young's modulus or with the shear modulus. The dynamic Poisson's ratio may be calculated from seismic compressional- (Vp) and shear-wave (Vs) velocities. From these dynamic moduli, the static moduli, which should be used in the crack models presented below, can often be inferred. However, because direct shear-wave velocity measurement in young ocean crust is difficult, especially in the uppermost part of the crust, the dynamic Poisson's ratio is largely unknown [Shaw, 1994]. One is therefore compelled to rely on a static Poisson's ratio determined from laboratory measurements of basalt as an approximation of the in-situ value. The commonly assumed Poisson's ratio for oceanic crust, based on the laboratory measurements of Christensen [1978], is 0.3 (yielding Vp/Vs = 1.9). However, the amplitude modeling of the on-bottom seismic refraction data of Christeson et al. [1994; 1997] near 9° 30'N indicates a Poisson's ratio at the seafloor ranging from 0.43 to 0.49 (i.e., Vp/Vs > 3). This value is similar to other determinations of Poisson's ratio for young oceanic crust, which fall in the range of 0.39 to 0.46 [Diachok et al., 1984; Harding et al., 1989; Vera et al., 1990]. These higher values of Poisson's ratio are more common for material dominated by thin cracks (i.e., aspect ratios much less than one) than by material dominated by more equidimensional voids, such as vesicles or interpillow voids [Jaeger and Cook, 1979; Shearer, 1988].
The dynamic Young's modulus, Ed, is given by Jaeger and Cook [1979] as:
Ed = Vp2 [rho](1+[nu])(1-2[nu]) / (1-[nu])
where Vp is P-wave velocity, [nu] is Poisson's ratio and [rho] is rock density. For the purposes of this chapter, Vp is the average P-wave velocity and [rho] is the average rock density of the uppermost 1 km of crust at the EPR, 9° 12'-54'N. The relationship between Ed and the static Young's modulus (Es) is somewhat complex and depends on the rock in question [Cheng and Johnston, 1981; Eissa and Kazi, 1988]. In general, because cracks propagate much more slowly than the velocities of seismic waves, the static Young's modulus (as well as the static Poisson's ratio) should be used [Gudmundsson, 1983; Gudmundsson, 1990]. In laboratory measurements the Ed/Es ratio is commonly around 2.0 [Cheng and Johnston, 1981], but for in-situ measurements this ratio ranges from 1.5 to 9.1 for common extrusive rocks [Gudmundsson, 1990; Link, 1968]. Because in-situ measurements in the Tertiary and Quaternary lava piles of Iceland suggest a ratio of 2.0 [Forslund and Gudmundsson, 1991; Gudmundsson, 1988], Wright et al. [1995b] adopted the same Ed/Es ratio for their estimates of fissure depth at the EPR 9° N. A static shear modulus, Gs, is given by Jaeger and Cook [1979]:
Gs = E / 2 (1+[nu])
Tensile Stress
Most MOR fissures are known to be vertical at the surface and must be generated by absolute tensile stresses (i.e., they are Mode I cracks; Figure 1). Under most loading conditions, absolute tensile stresses attain their peak values at the surface, so it is likely that all fissures form as tensile fractures at or near the surface, while with downward propagation some may subsequently change into normal faults [Opheim and Gudmundsson, 1989; Wright et al., 1995b]. Gudmundsson [1983] has shown that it is possible to estimate tensile stress during crack formation from Young's modulus, Poisson's ratio, and the length/width ratios of the cracks. On the EPR at 9° N Wright et al. [1995b] found that the length/width ratio for a small population of fissures resulted in a tensile stress estimate of 30 + 10 MPa, which is similar to estimates used by Lachenbruch [1973] and Macdonald et al. [1991]. In Iceland's Krafla fissure swarm, estimates range from 12 to 134 MPa, with an average of 20-30 MPa [Opheim and Gudmundsson, 1989]. Therefore, any crack formation model for the MOR must be able to generate tensile stresses on at least the order of ~20-40 MPa, or, alternatively, explain how existing crack width:length ratios might be overestimated.
Tensile Strength
No in situ values of tensile strength have been published for the MOR, but estimates suggest that it is very low. The best determinations currently available for volcanic rift zone environments range from 1 MPa to 6 MPa, with an inaccuracy of a factor 2, based on the work of Haimson and Rummel [1982] in Iceland. Fortunately this range covers the possible inaccuracy in ignoring the potential effects of pore-fluid pressure on crack formation which have not been rigorously quantified for the MOR. The general effect of pore-fluid pressure is to increase the probability of failure in a rock . Pore-fluid pressure affects only the normal stress, not the shear stress (A. Gudmundsson, personal communication, 1995).
Fissure Length, Width and Depth
On the MOR fissure length is determined fairly easily from side-scan sonar surveys (e.g., Edwards et al. [1991], Carbotte and Macdonald [1992], and Macdonald et al. [1992]) and fissure width can, in principle at least, be determined from near-bottom camera observations (e.g., Gente et al. [1986] andWright et al. [1995a]), although this has rarely been reported. Nur [1982] found that in tension crack systems the length of cracks should normally be equal to, or greater than, their depths. This is assuming, however, that the applied tensile stress increases with depth, which may not be entirely appropriate for MORs. Wright et al. [1995b] employed a slightly different model assuming that the width of a crack may be controlled by either its depth or its length (Figure 1). In order to know which is the minimum or width-controlling dimension, their model drew on the reasoning of Gudmundsson and Bäckström [1991], and Gudmundsson [1992]: (1) use the Griffith crack criterion [Griffith, 1924] to estimate the maximum possible depth of absolute tension in the crust; (2) compare this depth with an estimate of average length for the cracks under consideration; (3) if cracks are generally longer than this depth, then crack depth is the minimum and thus the width-controlling dimension, and the model applies. Returning to formula (2), substituting -[Tau]0 for [sigma]3 gives:
[sigma]1 <= 3[Tau]0
If [sigma]1 = [rho]gz then
[Tau]0 = [rho]gz / 3
and solving for depth z gives:
zmax = 3 [Tau]0 / [rho]g
where zmax is the maximum depth of absolute tension in the crust. Gudmundsson and Bäckström [1991] report an average zmax of 500 m for Holocene fissures in the rift zone of Iceland and find that most large-scale tension cracks should develop into normal faults at crustal levels deeper than 500-800 m. Wright et al. [1995b] calculated a zmax of 400 + 100 m for the EPR 9° 12'-54'N.
The length of fissures on the EPR at 9° N ranges from ~30 to ~650 m with an average length of ~170 m, based on the Argo I sonar data of Wright et al. [1995a]. Many of the cracks in general are rubble-filled, and many, if not most, of the shorter cracks are part of arrays, with the distances between the ends of the cracks being much shorter than the lengths of the cracks themselves. These arrays behave in a mechanical fashion essentially as a single crack. It is therefore surmised that those cracks are generally longer than zmax , the inferred maximum depth of absolute tension. So Wright et al. [1995b] employed the following fracture mechanics model to estimate crack depth from crack width:
zo = E w / [rho]V1(d/b)
where V1(d/b) is the stress function of Tada et al. [1973], which has 1% accuracy for any d/b:
V1(d/b) = 1.46 + 3.42 [1 - cos (pi/2) d/b ] / [ cos (pi/2) d/b ]2
In the stress function above, d is 400 m, in accordance with the earlier estimate of zmax, and b is the brittle thickness of the crust, which would be the depth to the 600° isotherm on a fast-spreading axis. This translates to ~1200 m for the EPR at 9-10° N [Lin and Parmentier, 1989]. The average depth to the axial magma chamber (AMC) reflector for the EPR at 9-10° N is just below this at ~1600 m [Kent et al., 1993]. This model predicts depths between ~60-275 +/- 40 m, including cracks that may penetrate the Layer 2A/2B boundary north of 9° 42'N, where crack widths are the greatest [Wright et al., 1995b]. These cracks are also located where the 1991 eruption of the ridge crest occurred at ~9° 45'-52'N [Haymon et al., 1993]. In general, these crack depths are comparable to the depths directly observed in the eroded Tertiary and Pleistocene lava piles of the rift zone in southwest Iceland [Gudmundsson, 1987; Forslund and Gudmundsson, 1991], and to those inferred for the Holocene pahoehoe lava flows of the rift zone in northeast Iceland [Gudmundsson and Bäckström, 1991], which range in depth from 200-400 m.
Models of Fissure Development
The development of fissures in volcanic rift zones on land has been attributed mainly to tensile stresses generated either by magmatic intrusions or by divergent plate motion. Current models of fissure formation are similar for the MOR where most workers agree that the presence of fissures is due to either: (a) lithospheric stretching (amagmatic, tensile cracking near-axis as the ridge accelerates from zero velocity to its full spreading rate, resulting in tectonic fissures); (b) magmatic intrusion (extensional cracking on-axis in the crust overlying dikes, resulting in eruptive fissures); or (c) thermal contraction of aging crust where tension cracks result from the shrinkage of cooling rock. Models have been proposed in the literature for both lithospheric stretching and magmatic intrusion, and are evaluated below.
A simple plate motion model (Figure 2) assumes that tensile stress due to far-field plate motion builds up gradually within the rift zone until new fissures form, old ones propagate, and tensile stress is temporarily relaxed . This model is also very attractive, as there is undoubtedly relative tensile stress that builds up within the MOR rift zone. However, because we are now aware of the importance of diking within the neovolcanic zone, particularly in the crust directly above a magma reservoir, a model invoking diking seems more appropriate, particularly within an axial summit trough. A plate motion model would be especially appropriate outside of an axial summit trough, within ~1-2 km of the axis.
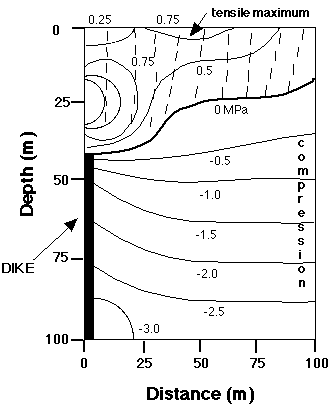
|
Fig. 2.
Simple plate motion model of fissure development after
Björnsson [1985], based on the 1975 rifting episode in the Krafla
region of NE Iceland. Tension is gradually built up in the axial rift zone by
ridge push forces and then is released every few years to few centuries in a
rifting episode, accompanied by the intrusion of magma into fissures in the
crust. Arrows are proportional to deviatoric stress in the crust.
|
Fissure Distribution
Several studies have included mapping of the distribution and orientation of fissuring on MOR crests spreading at different rates (e.g., Normark [1976], Luyendyk and Macdonald [1977], Gente et al. [1986], Kappel and Ryan [1986], USGS [1986], Crane [1987], Edwards et al. [1991], Embley et al. [1991], Hey et al. [1992], andWright et al. [1995a] which derives fissure distribution from the first segment-scale, continuous visual survey ever provided for a MOR crest). All of these studies agree on the following spatial and temporal aspects of fissure distribution: (1) most fissuring occurs primarily on the crest of the MOR in a 1- to 2-km wide region within the neovolcanic zone; (2) lengths and widths of fissures are generally 10-500 m and 0.2-3 m respectively; (3) orientations are largely sub-parallel to the adjacent ridge axis; and, (4) spacings are usually <100 m. Where the ridge has recently erupted, axial fissures formed by these mechanisms may be filled or covered by new, uncracked lava flows. Such contact relationships have been commonly observed in areas where very recent eruptions have been documented such as at the CoAxial site at 46° -47°N on the JdFR [Embley et al., 1993] and at the EPR at 9° -10°N [Haymon et al., 1993].
New Data from the Southern East Pacific Rise
(this section appears in web version of manuscript only)
Preliminary fissure distributions from the Sojourn Leg 2 (October-December, 1996) cruise to the southern EPR (SEPR) are presented here. The cruise involved an Argo II/AMS 120 survey of the narrow axial zone of the superfast-spreading SEPR at 17-18° S [Haymon et al., in prep.]. The AMS 120 was towed at an average height of ~75 m above the seafloor to collect high resolution, 120 kHz sidescan and bathymetry, the idea being to precisely locate the axial zone in this superfast spreading environment (17 cm/yr; Mammerickx et al. [1975]) so that it would be known how closely to space the Argo II tracklines. Argo II was then towed at an average height of 9 m above the seafloor to map hydrothermal vents, fissures, fault scarps, lava flow ages and morphologies, and biological communities with video, 35 mm, electronic still camera imagery, as well as with 200 kHz sidelooking sonar, a 675 kHz downlooking scanning sonar, and a CTD. Fifteen 45 km-long, axis parallel lines through the axial zone with line spacings of 10-30 m provided 100% saturation coverage where the axial zone is less than 100 m wide, down to a minimum coverage of 45% where the axial zone widens to 400 m (Figure 4). The major goal of the survey was to test the hypothesis (based on Argo I data from the EPR at 9-10° N) that along-strike thermal gradients set up by the segmented pattern of magma supply to fast-spreading MORs exert primary control on the distribution and types of hydrothermal vents and vent biota, as well as on variations in fissuring and other fine-scale volcanotectonic characteristics along the axial zone. Along a segment of ridge only 45 km long, the seismic data of Detrick et al. [1993] show that the AMC changes along-strike from a flat-topped body at relatively constant depth to a peaked cupola ("spike") that intrudes to within 800 m of the seafloor at ~17° 25'-27'S, contrasting with the flat-topped AMC at the EPR 9-10°N and representing the most extreme along-strike variation in thermal gradients known to exist on the MOR. At the time of this writing, AMS 120 sidescan and bathymetry, as well as Argo II video observations and sonar data are still being processed. However, preliminary data are now available and with the consistent along-strike trackline coverage throughout ~95% of the survey area (Figure 4), a preliminary assessment of fissure and lava age distributions are possible. Fissure density (abundance per square kilometer of seafloor imaged) maps, as well as fissure width determinations and depth estimates are forthcoming [Wright et al., in prep.].
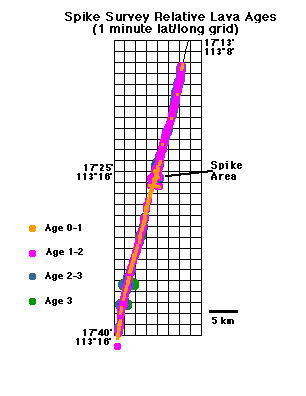
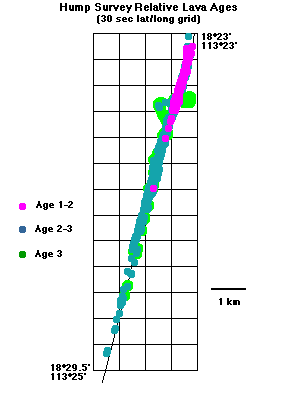
|
Fig. 5.
Maps showing the approximate, along-strike distribution of
relative axial lava ages in the "Spike" and "Hump" areas surveyed
with Argo II. Map projection is Mercator.
|
Figure 6 shows a pattern of abundant fissures in the northern portion of the survey area trending to fewer fissures south. As was found on the EPR at 9-10° N [Haymon et al., 1991; Wright et al., 1995a], the most densely fissured regions lie within older (Age 2) terrains while the least fissured areas coincide with where the freshest lavas are found, particularly just south of the "Spike" region at 17° 25'S (Figure 6).
The high rates of processes on the SEPR, such as spreading and crustal formation, beg the question of whether volcanotectonic events become larger and more intense, or simply much more frequent [Mottl et al., 1996]. And perhaps the along-strike demarcation between portions of ridge segments that are controlled more by tectonic than magmatic processes will not be as clear. How closely will the along-strike variability in crustal fissuring and other fine-scale features of the seafloor correspond to any 4th-order morphotectonic segmentation of the ridge crest? What will be the spatial and temporal constraints on volcanic-hydrothermal-tectonic cycling? Analyses of the Sojourn 2 fissure data in relation to the hydrothermal and magmatic data are still in progress, but we hope to provide more insight by late 1998.
Oceanic crust is produced at the ridge in a neovolcanic zone 1-2 km wide and is subsequently fissured and tectonized by normal faults within 2-3 km of the ridge axis . The process by which the faults grow along-strike is poorly known, but is thought to involve the formation of a set of open tension cracks which then link and coalesce to form the slip surface . Cowie and Scholz [1992a] model fault growth in terms of an inelastic deformation zone at the fault tip where cracking and frictional wear of the rock produce the mature fault surface. Their model predicts a linear relation between fault length and maximum displacement, and a tapered displacement profile instead of the elliptical one produced by a simple linear elastic fracture mechanics model. The proportionality constant between fault length and displacement is a function of the rock's shear strength divided by its shear modulus. Walsh and Watterson [1988] and Marrett and Allmendinger [1991] have found a non-linear relationship between fault length and maximum displacement. Cowie and Scholz [1992b] note that this non-linearity may be due to the small scale over which the observations were made or inappropriately combining of data from different environments (i.e., with different rock properties). Studies are in progress on the Mid-Atlantic Ridge (MAR) (e.g., Shaw and Kleinrock [submitted]) and on the Juan de Fuca Ridge (JdFR) [e.g., Wright, Embley, and Chadwick [in prep.]) and on the Juan de Fuca Ridge (JdFR) (e.g., Wright, Embley, and Chadwick[in prep.]) with data that span a much greater scale range for faults in a single tectonic environment and rock type to resolve these divergent results.
Compared with fissures, most MOR normal faults are large and grade into tension fractures at their ends . This would indicate that MOR fissures have to attain a certain minimum length and/or depth in order to develop into normal faults. In Iceland, Opheim and Gudmundsson [1989] define normal faults as fissures having vertical displacement in excess of 1 m. Their results indicate that a fissure has to attain a length of several hundred meters before any significant vertical displacement occurs. Similarly on the EPR at 9° N Wright et al. [1995b] found that a fissure has to attain a width of ~5-10 m and a subsequent depth of ~400 m before potentially changing into a normal fault, at which point the tension crack would tend to close. However, such a fissure may have to be carried out of the neovolcanic zone by divergent plate motion before changing to a normal fault. Edwards et al. [1991] and Carbotte and Macdonald [1994] have shown that normal faulting is not common on fast-spreading ridges within + 3 km of the ridge axis because the lithosphere is too thin and weak to support it. Furthermore, Chen and Morgan [1990] point out that near-axis faulting may be impeded at fast-spreading ridges because the crust is decoupled from extensional stresses by an axial magma chamber (AMC). On slow-spreading ridges the lithosphere is sufficiently thick and strong enough to support normal faulting right along the axis, and such faults may extend all the way to the base of the crust (e.g., Macdonald and Luyendyk [1977], Huang and Solomon [1988], and Kong et al. [1992]).
Tectonic Versus Eruptive Fissuring: Linkages to Ridge Segmentation and Magmatism
The finest scale of ridge segmentation (fourth order) probably corresponds to individual fissure eruption events. For example, at this very fine scale on the EPR, excellent correlations can be seen within individual fourth order segments between lava age, density and width of fissuring, and hydrothermal vent abundance [Haymon et al., 1991; Wright et al., 1995a]. See Langmuir et al. [1986] or Macdonald et al. [1991] for definitions of ridge segmentation, orders 1-4.
For example, at the EPR 9° N, Wright et al. [1995a] found the widest cracks to be in the youngest lavas suggesting that these cracks are eruptive in origin and control the locations of high-temperature hydrothermal venting during the early stages of the volcanic-hydrothermal-tectonic cycle. Once dikes are emplaced in crust that is already subject to external tensile stress (related to divergent plate motion), tensile stress concentration in portions of the crust directly above the tops of these dikes should already be high enough to form the wide cracks. Also, the thickness of these dikes must be at least 2-3 m. Dike thickness is proportional to dike dimension and driving pressure (the difference between the magma pressure in the dike and the regional least compressive stress): the thicker the dike the greater the driving pressure, and the wider the fissure forming above it [Rubin and Pollard, 1987]. So at the very outset these fissures are wide and deep, remaining so until they are carried away from the neovolcanic zone by divergent plate motion. If their widths increased with time within the neovolcanic zone so would their depths, and eventually, at crustal depths of 500-800 m [Gudmundsson and Bäckström, 1991], the cracks would change into normal faults and thereby tend to close at the surface. And although all fissures provide pathways for seawater to enter the crust, which might potentially cool the hydrothermal and magmatic systems, most hydrothermal heat loss in the axial zone of fast-spreading centers probably occurs early along the wide, deep, eruptive fissures.
In contrast to these sparse eruptive fissures in younger lavas, narrower, shallower cracks occurring in older, colder crust on the EPR probably accumulate with time in response to tensile stresses. These shallower cracks do not tap magma and typically are not hydrothermally active. They are primarily tectonic in origin, forming in response to crustal extension.
The direct proportionality of crack depth to crack width presented in Wright et al. [1995b] adds to other observational evidence indicating that wide fissures in relatively young lava flows are primarily eruptive and are thus deep enough to facilitate the flux of magma and fluids from the tops of the feeder dikes during an eruption event (Figure 7). Alvin observations of the 1991 eruption site on the EPR at 9° N confirm that many wide fissures there may be eruptive in origin, and numerous high-temperature, vapor-rich vents are localized along the margins of these wide fissures [Haymon et al., 1993]. Haymon et al. [1993] proposed the intrusion of dikes to ~200 m beneath the floor of the axial summit caldera during the eruption, which drove the phase separation of hydrothermal fluids near the tops of the dikes and a large flux of vapor-rich fluids through the overlying rubbly lavas. A possible origin for these dikes is the inflation of the AMC due to the injection of melt from the upper mantle. In the magmatic pressure change model of Gudmundsson [1987], magma accumulation and slight increases in magmatic pressure within the AMC prior to an eruption cause uplift and bending of the overlying crust, thereby generating tensile stress in the upper part of the crust sufficiently large enough to form cracks. During uplift and bending, the potential tensile stress is much higher than during ordinary divergent plate motion, resulting in cracks at the leading edge of these dikes that may be exceptionally wide and deep.
Related to the segmentation of the MOR is the cycling of processes at the ridge axis. The structure of the ridge crest is related to both magmatic and tectonic processes that may be cyclic within a 2nd-, 3rd- or fourth-order ridge segment. Volcanic-tectonic cycles have been proposed in previous studies of the JdFR [Lichtman and Eissen, 1983; Embley et al., 1991], the EPR (e.g., Gente et al. [1986] andHaymon et al. [1991]) the MAR (e.g., Eberhart et al. [1988] and Fouquet et al. [1993]), and the Galapagos Rift (e.g., Embley et al. [1988]).
On the fast-spreading EPR, fine-scale volcanic, tectonic, and hydrothermal characteristics of the axial zone strongly reflect the processes of ridge segmentation on both a second- and a fourth-order scale. The distribution of fine-scale features have spatially and temporally constrained the model of Haymon et al. [1991] in which the individual fourth-order segments are in different phases of a volcanic-hydrothermal-tectonic cycle that begins with cracking/diking and eruptive fissuring, followed by magmatic drainback, gravitational collapse, possible development of an ASC, and then cooling of the heat source, initiation of tectonic fissuring, and waning of hydrothermal and magmatic activity (Figure 10). At the end of the cycle, hydrothermal activity ceases, and cold tectonic cracking as well as mass wasting that widens the ASC, are the dominant processes modifying the axial zone.
A second important observation is that along-strike variability in crustal fissuring and other fine-scale features of the seafloor correspond to the fourth-order morphotectonic segmentation of the ridge crest [Haymon et al., 1991]. The tendency of fourth-order segment boundaries to coincide with along-strike changes in the mean density of fissuring, in relative ages of axial lavas, and in hydrothermal vent abundances supports the premise of Haymon et al. [1991] that each fourth-order segment is in its own phase of a volcanic-hydrothermal-tectonic cycle. Such a cycle would begin with cracking/diking and eruptive fissuring, followed by magmatic drainback, gravitational collapse, possible development of an ASC, and then cooling of the heat source, initiation of tectonic fissuring, and waning of hydrothermal and magmatic activity. At the end of the cycle, hydrothermal activity ceases, and cold tectonic cracking as well as mass wasting that widens the ASC, are the dominant processes modifying the axial zone [Haymon et al., 1991; Wright et al., 1995a].
Conclusion: Directions for Future Research
Detailed studies of both axial and near-axial regions of the EPR and SEPR, as well as the MAR, JdFR, the Indian Ocean Ridges, and the Galapagos Rift will continue to provide many insights into MOR geological processes. However, a number of first-order geological problems remain to be solved. Among these is the determination of the influence of axial tectonic activity (which includes crustal cracking) on the evolution of crustal morphology and physical properties. Specific questions include the following:
The critically important parameters of fissure abundance, spacing, length, width, and depth have rarely been reported anywhere on the seafloor, with the exception of the fast-spreading EPR, and have only recently been perceived as important in marine geology [Johnson, 1990]. The research agendas being set at various international workshops (e.g., Purdy and Fryer [1990], Dziewonski and Lancelot [1995], and Mottl et al. [1996]) are now including the determination of these parameters as a high priority for morphotectonic studies of MOR crust, certainly for any study that hopes to more fully understand the nature of extensional failure of the ocean crust. Clearly we need to continue "breaking new ground" with more fine-scale surveys and quantitative studies of axial and off-axial fissures as they relate to faulting and magmatism along the global MOR.
Acknowledgements. Many thanks to Rachel Haymon, Ken Macdonald, Agust Gudmundsson, Allan Rubin, and Dan Scheirer for helpful and encouraging discussions regarding the ideas expressed in this paper. Thanks to Dan Scheirer for supplying the SEPR Sea Beam 2000 grids and to Rachel Haymon for the Argo II data. The critical reviews of Agust Gudmundsson and an anonymous referee significantly improved the manuscript. This work was supported by National Science Foundation grant OCE-9521039.
References
Anderson, T.L., Fracture Mechanics: Fundamentals and Applications, 688 pp., CRC Press, Inc., Boca Raton, Florida, 1995.
Auzende, J.-M., V. Ballu, R. Batiza, D. Bideau, J.-L. Charlou, M.-H. Cormier, Y. Fouquet, P. Geistodoerfer, Y. Lagabrielle, J. Sinton, and P. Spadea, Recent tectonic, magmatic, and hydrothermal activity on the East Pacific Rise between 17° S and 19° S: Submersible observations, J. Geophys. Res., 101, 17,995-18,010, 1996.
Bieniawski, Z.T., Mechanism of brittle fracture of rock. Part 1, Theory of the fracture process., Int. J. Rock Mech. Min. Sci., 4, 395-406, 1967.
Björnsson, A., Dynamics of crustal rifting in Iceland, J. Geophys. Res., 90, 10,151-10,162, 1985.
Carbotte, S., and K. C. Macdonald, East Pacific Rise 8° -10° 30'N: Evolution of ridge segments and discontinuities from SeaMARC II and three-dimensional magnetic studies, J. Geophys. Res., 97, 6959-6982, 1992.
Carbotte, S.M., and K.C. Macdonald, Comparison of seafloor tectonic fabric at intermediate, fast, and super fast spreading ridges: Influence of spreading rate, plate motions, and ridge segmentation on fault patterns, J. Geophys. Res., 99, 13,609-13,631, 1994.
Cartwright, J.A., B.D. Trudgill, and C.S. Mansfield, Fault growth by segment linkage: An explanation for scatter in maximum displacement and trace length data from the Canyonlands Grabens of SE Utah, J. Struct. Geol., 17, 1319-1326, 1995.
Chen, Y., and W.J. Morgan, Rift valley/no rift valley transition at mid-ocean ridges, J. Geophys. Res., 95, 17,571-17,581, 1990.
Cheng, C. H., and D. H. Johnston, Dynamic and static moduli, Geophys. Res. Lett., 8, 39-42, 1981.
Christensen, N. I., Ophiolites, seismic velocities and oceanic crustal structure, Tectonophysics, 47, 131-157, 1978.
Christeson, G.L., G.M. Purdy, and G.J. Fryer, Seismic constraints on shallow crustal emplacement processes at the fast-spreading East Pacific Rise, J. Geophys. Res., 99, 17,957-17,996, 1994.
Christeson, G.L., P.R. Shaw, and J.D. Garmany, Shear and compressional wave structure of the East Pacific Rise, 9° -10° N, J. Geophys. Res., 102, 7821-7836, 1997.
Cowie, P. A., and C. H. Scholz, Displacement length scaling relationship for faults: Data synthesis and discussion, J. Struct. Geol., 14, 1149-1156, 1992a.
Cowie, P. A., and C. H. Scholz, Physical explanation for the displacement length relationship of faults using a post-yield fracture mechanics model, J. Struct. Geol., 14, 1133-1148, 1992b.
Cowie, P.A., A. Malinverno, W.B.F. Ryan, and M.H. Edwards, Quantitative fault studies on the East Pacific Rise: A comparison of sonar imaging techniques, J. Geophys. Res., 99, 15,205-15,218, 1994.
Crane, K., Structural evolution of the East Pacific Rise axis from 13° 10'N to 10° 35'N: Interpretations from SeaMARC I data, Tectonophysics, 136, 65-124, 1987.
Detrick, R.S., A.J. Harding, G.M. Kent, J.A. Orcutt, and J.C. Mutter, Seismic structure of the southern East Pacific Rise, Science, 259, 499, 1993.
Diachok, O. I., R. L. Dicus, and S. C. Wales, Elements of a geoacoustic model of the upper crust, J. Acoust. Soc. Am., 75, 324-334, 1984.
Dziak, R.P., C.G. Fox, and A.E. Schreiner, The June-July 1993 seismo-acoustic event at CoAxial segment, Juan de Fuca Ridge: Evidence for a lateral dike injection, Geophys. Res. Lett., 22, 135-138, 1995.
Dziewonski, A., and Y. Lancelot, Multidisplinary Observatories on the Deep Seafloor, 229 pp., INSU/CNRS/IFREMER/USSAC/ODP, Marseille, France, 1995.
Eberhart, G. L., P. A. Rona, and J. Honnorez, Geologic controls of hydrothermal activity in the Mid-Atlantic Ridge rift valley: Tectonics and volcanics, Mar. Geophys. Res., 10, 233-259, 1988.
Edwards, M. H., D. J. Fornari, A. Malinverno, W. B. F. Ryan, and J. Madsen, The regional tectonic fabric of the East Pacific Rise from 12° 50'N to 15° 10'N, J. Geophys. Res., 96, 7995-8018, 1991.
Eissa, E. A., and A. Kazi, Relation between static and dynamic Young's modulus, Int. J. Rock Mech. Min. Sci. Geomech. Abstr., 25, 479-482, 1988.
Embley, R. W., I. R. Jonasson, M. R. Perfit, J. M. Franklin, M. A. Tivey, A. Malahoff, M. F. Smith, and T. J. G. Francis, Submersible investigations of an extinct hydrothermal system on the Galapagos Ridge: Sulfide mounds, stockwork zone, and differentiated lavas, Can. Mineral., 26, 517-539, 1988.
Embley, R. W., W. Chadwick, M. R. Perfit, and E. T. Baker, Geology of the northern Cleft segment, Juan de Fuca Ridge: Recent lava flows, sea-floor spreading, and the formation of megaplumes, Geology, 19, 771-775, 1991.
Embley, R. W., I. R. Jonasson, S. Petersen, G. Massoth, D. Butterfield, V. Tunnicliffe, T. Parker, K. Juniper, J. Sarrazin, W. W. Chadwick, A. Bobbitt, and J. Getsiz, Investigations of recent eruptive sites on the Juan de Fuca Ridge using the ROPOS: Revisits to the North Cleft 1980s eruption area and a fast response to a June/July eruption on the CoAxial Segment (abstract), Eos, Trans. AGU, 74, 561, 1993.
Forslund, T., and A. Gudmundsson, Crustal spreading due to dikes and faults in southwest Iceland, J. Struct. Geol., 13, 443-457, 1991.
Fouquet, Y., A. Wafik, P. Cambon, C. Mevel, G. Meyer, and P. Gente, Tectonic setting and mineralogical and geochemical zonation in the Snake Pit sulfide deposit (Mid-Atlantic Ridge at 23° N), Econ. Geol., 88, 2018-2036, 1993.
Francheteau, J., R. Armijo, J.L. Cheminee, R. Hekinian, P. Lonsdale, and N. Blum, 1 Ma East Pacific Rise oceanic crust and uppermost mantle exposed by rifting in Hess Deep (equatorial Pacific Ocean), Earth Planet. Sci. Lett., 101, 281-295, 1990.
Gente, P., J. M Auzende, V. Renard, Y. Fouqet, and D. Bideau, Detailed geological mapping by submersible of the East Pacific Rise axial graben near 13° N, Earth Planet. Sci. Lett., 78, 224-236, 1986.
Goldstein, S.J., M.R. Perfit, R. Batiza, D.J. Fornari, and M.T. Murrell, Off-axis volcanism at the East Pacific Rise detected by Uranium-series dating of basalts, Nature, 367, 157-159, 1994.
Gregg, T.K.P., Investigating submarine volcanic eruption dynamics: Comparative field studies and developing methodologies, RIDGE Events, 8, 1-4, 1997.
Gregg, T.K.P., D.J. Fornari, M.R. Perfit, R.M. Haymon, and J.H. Fink, Rapid emplacement of a mid-ocean ridge lava flow on the East Pacific Rise at 9° 46'-51'N, Earth Planet. Sci. Lett., 144, E1-E8, 1996.
Griffith, A. A., The phenomena of rupture and flow in solids, Philos. Trans. R. Soc. London, 221, Ser. A, 163-197, 1920.
Griffith, A. A., Theory of rupture, in Proceedings of the First International Congress on Applied Mechanics, edited by C. B. Biezeno and J. M. Burgers, 55-63, Waltman, Delft, 1924.
Grindlay, N. R., P. J. Fox, and P. R. Vogt, Morphology and tectonics of the Mid-Atlantic Ridge (25° -27° 30'S) from Sea Beam and magnetic data, J. Geophys. Res., 97, 6983-7010, 1992.
Gudmundsson, A., Form and dimension of dykes in eastern Iceland, Tectonophysics, 95, 295-307, 1983.
Gudmundsson, A., Geometry, formation and development of tectonic fractures on the Reykjanes Peninsula, southwest Iceland, Tectonophysics, 139, 295-308, 1987.
Gudmundsson, A., Effect of tensile stress concentration around magma chambers on intrusion and extrusion frequencies, J. Volcanol. Geotherm. Res., 35, 179-194, 1988.
Gudmundsson, A., Emplacement of dikes, sills, and crustal magma chambers at divergent plate boundaries, Tectonophysics, 176, 257-275, 1990.
Gudmundsson, A., Formation and growth of normal faults at the divergent plate boundary in Iceland, Terra Nova, 4, 464-471, 1992.
Gudmundsson, A., Infrastructure and mechanics of volcanic systems in Iceland, J. Volcanol. Geotherm. Res., 64, 1-22, 1995.
Gudmundsson, A., and K. Bäckström, Structure and development of the Sveinagja Graben, Northeast Iceland, Tectonophysics, 200, 111-125, 1991.
Haimson, B. C., and F. Rummel, Hydrofracturing stress measurements in the Iceland research drilling project drill hole at Reydarfjördur, Iceland, J. Geophys. Res., 87, 6631-6649, 1982.
Harding, A. J., J. A. Orcutt, M. E. Kappus, E. E. Vera, J. C. Mutter, P. Buhl, D. R. S., and T. M. Brocher, Structure of young oceanic crust at 13° N on the East Pacific Rise from expanding spread profiles, J. Geophys. Res., 94, 1989.
Haymon, R. M., D. J . Fornari, M. H. Edwards, S. Carbotte, D. Wright, and K. C. Macdonald, Hydrothermal vent distribution along the East Pacific Rise crest (9° 09'-54'N) and its relationship to magmatic and tectonic processes on fast-spreading mid-ocean ridges, Earth Planet. Sci. Lett., 104, 513-534, 1991.
Haymon, R., D. Fornari, R. Lutz, M. Perfit, K. Macdonald, K. Von Damm, M. Lilley, W. C. I. Shanks, D. Nelson, M. Edwards, M. Kappus, D. Colodner, D. Wright, D. Scheirer, M. Black, H. Edmonds, E. Olson, and T. Geiselman, Dramatic short-term changes observed during March '92 dives to April '91 eruption site on the East Pacific Rise (EPR) crest, 9° 45-52'N (abstract), Eos Trans. AGU, 43, 524, 1992.
Haymon, R. M., D. J. Fornari, K. L. Von Damm, M. D. Lilley, M. R. Perfit, J. M. Edmond, W. C. Shanks III, R. A. Lutz, J. B. Grebmeier, S. Carbotte, D. Wright, E. McLaughlin, E. Smith, N. Beedle, and E. Olson, Volcanic eruption of the mid-ocean ridge along the East Pacific Rise crest at 9° 45-52'N: 1. Direct submersible observations of seafloor phenomena associated with an eruption event in April, 1991, Earth Planet. Sci. Lett., 119, 85-101, 1993.
Hayward, N.J., and C.J. Ebinger, Variations in the along-axis segmentation of the Afar Rift system, Tectonics, 15, 244-257, 1996.
Head, J.W., III, L. Wilson, and D.K. Smith, Mid-ocean ridge eruptive vent morphology and substructure: Evidence for dike widths, eruption rates, and evolution of eruptions and axial volcanic ridges, J. Geophys. Res., 101, 28,265-28,280, 1996.
Helm, D.C., Hydraulic forces that play a role in generating fissures at depth, Bull. Assoc. Engr. Geol., 31, 293-304, 1994.
Hey, R.N., J.M. Sinton, M.C. Kleinrock, R.N. Yonover, K.C. Macdonald, S.P. Miller, R.C. Searle, D.M. Christie, T.M. Atwater, N.H. Sleep, H.P. Johnson, and C.A. Neal, ALVIN investigation of an active propagating rift system, Galapagos 95.5° W, Mar. Geophys. Res., 14, 207-226, 1992.
Huang, F., Z. Wang, and Y. Zhao, The development of rock fracture from microfracturing to main fracture formation, Int. J. Rock Mech. Min. Sci. & Geomech. Abstr., 30, 925-928, 1993.
Huang, P.Y., and S.C. Solomon, Centroid depths of mid-ocean ridge earthquakes: Dependence on spreading rate, J. Geophys. Res., 93, 13,445-13,477, 1988.
Hurst, S.D., J.A. Karson, and K.L. Verosub, Paleomagnetism of tilted dikes in fast spread oceanic crust exposed in the Hess Deep Rift: Implications for spreading and rift propagation, Tectonics, 13, 789-802, 1994.
Jaeger, J. C., and N. G. W. Cook, Fundamentals of Rock Mechanics, 3rd edition, Chapman and Hall, London, 1979.
Johnson, H. P., Tectonic regulation of the physical properties of the seafloor: The view from the Juan de Fuca Ridge, in Proceedings of a Workshop on the Physical Properties of Volcanic Seafloor, edited by G. M. Purdy and G. J. Fryer, 55-72, Woods Hole Oceanographic Institution, Woods Hole, MA, 1990.
Johnson, H.P., and B.L. Salem, Magnetic properties of dikes from the oceanic upper crustal section, J. Geophys. Res., 99, 21,733-21,740, 1994.
Kappel, E. S., and W. B. F. Ryan, Volcanic episodicity and a non-steady state rift valley along Northeast Pacific spreading centers: Evidence from Sea MARC I, J. Geophys. Res., 91, 13,925-13,940, 1986.
Karson, J.A., S.D. Hurst, and P. Lonsdale, Tectonic rotations of dikes in fast-spread oceanic crust exposed near Hess Deep, Geology, 20, 685-692, 1992.
Kent, G. M., A. J. Harding, and J. A. Orcutt, Distribution of magma beneath the East Pacific Rise between the Clipperton Transform and the 9° 17'N deval from forward modeling of common depth point data, J. Geophys. Res., 98, 13,945-13,970, 1993.
Kidd, R.G.W., A model for the process of formation of the upper oceanic crust, Geophys. J. R. Astron. Soc., 50, 149-183, 1977.
Kleinrock, M.C., and S.E. Humphris, Structural asymmetry of the TAG Rift Valley: Evidence from a near-bottom survey, Geophys. Res. Lett., 23, 3439-3442, 1996.
Kong, L.S., S.C. Solomon, and G.M. Purdy, Microearthquake characteristics of a mid-ocean ridge along-axis high, J. Geophys. Res., 97, 1659-1686, 1992.
Lachenbruch, A. H., A simple mechanical model for oceanic spreading centers, J. Geophys. Res., 78, 3395-3417, 1973.
Langmuir, C. H., J. F. Bender, and R. Batiza, Petrological and tectonic segmentation of the East Pacific Rise, 5° 30'N-14° 30'N, Nature, 322, 422-429, 1986.
Lichtman, G. S., and J.-P. Eissen, Time and space constraints on the evolution of medium-rate spreading centers, Geology, 11, 592-595, 1983.
Lin, J., and E. M. Parmentier, Mechanisms of lithospheric extension at mid-ocean ridges, Geophys. J., 96, 1-22, 1989.
Link, H., On the correlation of seismically and statically determined moduli of elasticity of rock masses, Felsmech. Ingenieurgeol., 4, 90-110, 1968.
Lowell, R.P., and L.N. Germanovich, Dike injection and the formation of megaplumes at ocean ridges, Science, 267, 1804-1807, 1995.
Luyendyk, B. P., and K. C. Macdonald, Physiography and structure of the inner floor of the FAMOUS rift valley: Observations with a deep-towed instrument package, Geol. Soc. Am. Bull., 88, 648-663, 1977.
Macdonald, K. C., Mid-ocean ridges: Fine scale tectonic, volcanic and hydrothermal processes within the plate boundary zone, Ann. Rev. Earth Planet. Sci., 10, 155-190, 1982.
Macdonald, K.C., and B.P. Luyendyk, Deep-tow studies of the structure of the Mid-Atlantic Ridge crest near lat 37° N, Geol. Soc. America Bull., 88, 621-636, 1977.
Macdonald, K., J.-C. Sempéré, and P. J. Fox, East Pacific Rise from Siqueiros to Orozco Fracture Zones: Along-strike continuity of axial neovolcanic zone and structure and evolution of overlapping spreading centers, J. Geophys. Res., 89, 6049-6069, 1984.
Macdonald, K. C., P. J. Fox, L. J. Perram, M. F. Eisen, R. M. Haymon, S. P. Miller, S. M. Carbotte, M.-H. Cormier, and A. N. Shor, A new view of the mid-ocean ridge from the behaviour of ridge-axis discontinuities, Nature, 335, 217-225, 1988.
Macdonald, K. C., D. S. Scheirer, and S. M. Carbotte, Mid-ocean ridges: discontinuities, segments and giant cracks, Science, 253, 986-994, 1991.
Macdonald, K. C., P. J. Fox, S. Carbotte, M. Eisen, S. Miller, L. Perram, D. Scheirer, S. Tighe, and C. Weiland, The East Pacific Rise and its flanks, 8° -17° N: History of segmentation, propagation and spreading direction based on SeaMARC II and Sea Beam studies, Mar. Geophys. Res., 14, 299-334, 1992.
Macdonald, K.C., P.J. Fox, R.T. Alexander, R. Pockalny, and P. Gente, Volcanic growth faults and the origin of Pacific abyssal hills, Nature, 380, 125-129, 1996.
Mammerickx, J., R.N. Anderson, H.W. Menard, and S.M. Smith, Morphology and tectonic evolution of the East Central Pacific, Geol. Soc. Am. Bull., 86, 111-118, 1975.
Mastin, L.G., and D.D. Pollard, Surface deformation and shallow dike intrusion processes at Inyo Craters, Long Valley, California, J. Geophys. Res., 93, 13,221-13,235, 1988.
Marrett, R., and R. W. Allmendinger, Estimates of strain due to brittle faulting: Sampling of fault populations, J. Struct. Geol., 13, 735-738, 1991.
Morton, J. L., N. H. Sleep, W. R. Normark, and D. H. Tompkins, Structure of the southern Juan de Fuca Ridge from seismic reflection records, J. Geophys. Res., 92, 11,315-11,326, 1987.
Mottl, M., E. Baker, K. Macdonald, J. Sinton, and G. Wheat, Processes and Fluxes on a Superfast Spreading Ridge: The Southern East Pacific Rise, RIDGE, Durham, NH, 36 pp., 1996.
Normark, W. R., Delineation of the main extrusion zone of the East Pacific Rise at Lat. 21° N, Geology, 4, 681-685, 1976.
Nur, A., The origin of tensile fracture lineaments, J. Struct. Geol., 4, 31-40, 1982.
Opheim, J. A., and A. Gudmundsson, Formation and geometry of fractures, and related volcanism, of the Krafla Fissure Swarm, Northeast Iceland, Geol. Soc. Am. Bull., 101, 1608-1622, 1989.
Perfit, M.R., D.J. Fornari, M.C. Smith, J.F. Bender, C.H. Langmuir, and R.M. Haymon, Small-scale spatial and temporal variations in mid-ocean ridge crest magmatic processes, Geology, 22, 375-379, 1994.
Pockalny, R. A., and P. J. Fox, Estimation of crustal extension within the plate boundary zone of slowly spreading mid-ocean ridges (abstract), Eos Trans. AGU, 70, 1300, 1989.
Pollard D. D., P. T. Delaney, W. A. Duffield, E. T. Endo, and A. T. Okamura, Surface deformation in volcanic rift zones, Tectonophysics, 94, 541-584, 1983.
Purdy, G. M., and G. J. Fryer, Proceedings of a Workshop on the Physical Properties of Volcanic Seafloor, Woods Hole Oceanographic Institution, Woods Hole, MA, 279 pp., 1990.
Rubin, A.M., Dike-induced faulting and graben subsidence in volcanic rift zones, J. Geophys. Res., 97, 1839-1858, 1992.
Rubin, A. M., and D. D. Pollard, Origins of blade-like dikes in volcanic rift zones, in Volcanism in Hawaii, vol. 2, edited by R. W. Decker, T. L. Wright, and P. H. Stauffer, pp. 1449-1470, U.S. Geol. Surv. Prof. Paper 1350, Denver, Colo., 1987.
Scheirer, D. S., M. Cormier, K. Macdonald, R. Haymon, and S. White, Sojourn Leg 1: Completing the picture of the East Pacific Rise and its flanks in the MELT area (abstract), Eos, Trans. AGU, 77, F663, 1996.
Scheirer, D. S., and K. C. Macdonald, Variation in cross-sectional area of the axial ridge along the East Pacific Rise: Evidence for the magmatic budget of a fast-spreading center, J. Geophys. Res., 98, 7871-7886, 1993.
Scholz, C. H., Mechanics of faulting, Ann. Rev. Earth Planet. Sci., 17, 309-334, 1989.
Schouten, H., K. D. Klitgord, and J. A. Whitehead, segmentation of mid-ocean ridges, Nature, 317, 225-229, 1985.
Sempéré, J.-C., and K. C. Macdonald, Deep-tow studies of the overlapping spreading centers at 9° 03'N on the East Pacific Rise, Tectonics, 5, 881-900, 1986.
Shaw, P. R., Age variations of oceanic crust Poisson's ratio: Inversion and a porosity evolution model, J. Geophys. Res., 99, 3057-3066, 1994.
Shaw, P.R., and J. Lin, Causes and consequences of variations in faulting style at the Mid-Atlantic Ridge, J. Geophys. Res., 98, 21,839-21,851, 1993.
Shaw, P.R., and M.C. Kleinrock, Growth and evolution of normal faults at the Mid-Atlantic Ridge at the TAG area, Geophys. Res. Lett., submitted.
Shearer, P. M., Cracked media, Poisson's ratio and the structure of the upper oceanic crust, Geophys. J. R. Astron. Soc., 92, 357-362, 1988.
Sigurdsson, O., Surface deformation of the Krafla fissure swarm in two rifting events, J. Geophys., 47, 154-159, 1980.
Tada, H., P. C. Paris, and G. R. Irwin, The Stress Analysis of Cracks Handbook, 383 pp., Del Research Corporation, Hellertown, Pennsylvania, 1973.
U.S. Geological Survey Juan de Fuca Study Group, Submarine fissure eruptions and hydrothermal vents on the southern Juan de Fuca Ridge: Preliminary observations from the submersible Alvin, Geology, 14, 823-827, 1986.
van Wyk de Vries, B., and O. Merle, The effect of volcanic constructs on rift fault patterns, Geology, 24, 643-646, 1996.
Vera, E. E., J. C. Mutter, P. Buhl, J. A. Orcutt, A. J. Harding, M. E. Kappus, R. S. Detrick, and T. M. Brocher, The structure of 0- to 0.2-m.y.-old oceanic crust at 9° N on the East Pacific Rise from expanded spread profiles, J. Geophys. Res., 95, 15,529-15,556, 1990.
Walsh, J. J., and J. Watterson, Analysis of the relationship between displacements and dimensions of faults, J. Struct. Geol., 10, 239-247, 1988.
Wright, D.J., R.M. Haymon, and D.J. Fornari, Crustal fissuring and its relationship to magmatic and hydrothermal processes on the East Pacific Rise crest (9° 12'-54'N), J. Geophys. Res., 100, 6097-6120, 1995a.
Wright, D.J., R.M. Haymon, and K.C. Macdonald, Breaking new ground: Estimates of crack depth along the axial zone of the East Pacific Rise (9° 12'-54'N), Earth Planet. Sci. Lett., 134, 441-457, 1995b.