
[ home port | lectures | labs | discussion | surf | email prof. ]

 Lab 1
Lab 1
Things to Get Out of This Lab:
Materials: Ruler or straight edge, pencils, calculator
Introduction
When you look at the earth, you see mountains, valleys, rivers, the ocean, etc. If you can't visit an area in person, you can experience it through a map! Maps are used to portray geographic data. These data may be locations of volcanoes, earthquakes, rock types, etc. You are already familiar with the use of maps to portray locations of countries cities, roads, etc. In this lab, you will learn about some of the important properties of maps. Oceanographers commonly use bathymetric maps (maps with contours of ocean depth) to describe and study the areas in which they work. We will use bathymetric maps for many purposes in this class.
Locations on the Earth: Latitude and Longitude
The Earth rotates about an axis passing through the North and South poles. Longitude lines (called meridians) divide the Earth into 360 equal sections (degrees) joining at the poles. Think of these as analogous to sections of an orange. Latitude lines (called parallels) divide the Earth into 180 equal angles perpendicular to lines of longitude. 0 degrees latitude is the equator. Latitudes north of the equators range from 0 to 90N (at the North Pole). Latitudes south of the equator range from 0 to 90S (at the South Pole). Longitude 0, the Prime Meridian, passes through Greenwich, England. To the west of Greenwich, lines of longitude go to 180W, and to the east of Greenwich they go to 180E, for a total of 360 degrees.
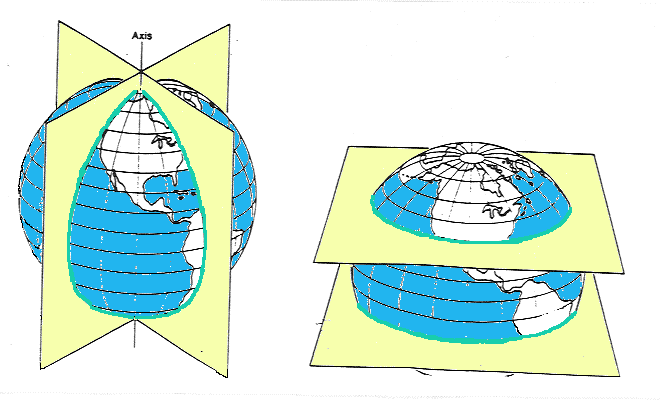
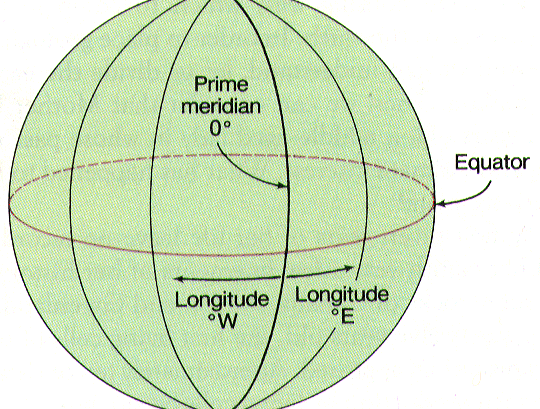
The point on the Earth's surface directly opposite Greenwich is the
International Date Line, the 180° meridian. In recording the location of a
point on the Earth's surface, it is necessary to specify north or south
latitude and east or west longitude. Corvallis lies at approximately 45° N
latitude and 123° W longitude, expressed as 45° N, 123° W.
One degree of latitude (in the north-south direction) equals 111 km or 60 nautical miles. One degree of longitude (in the east-west direction) equals this same distance ONLY AT THE EQUATOR. Longitudinal distance decreases toward the poles. Each degree of longitude and latitude is divided into 60 minutes (expressed as ` ), and each minute is divided into 60 seconds (expressed as " ). Using this higher degree of precision, the center of downtown Corvallis lies at 44° 33' 53"N, 123° 15' 39"W. In OC/GEO 103 labs, latitude and longitude values may sometimes be given in decimal degrees, rather than minutes and seconds.
Brain teasers: Where on the Earth's surface can you go due north 1 km, then due south 1 km, and not end up at the same point you started at?
How much distance separates each degree of longitude at the North Pole?
Distances Between Locations
The approximate distance between any 2 points on the surface of the Earth is an angular distance. Below is the formula to calculate the distance in nautical miles (nm). [Delta] means "change in" or differences in degrees of longitude or latitude between the 2 points:

The 2 in the formula is squared, not times 2. To calculate the distance in kilometers (km), use the same formula above, except substitute 111 km for 60 nm. The distances that you get from this formula are not exact because the values 60 nm or 111 km per degree of latitude (which we use in the formula) are average values. The earth is ellipsoidal (fatter at the equator), so the values of 111 and 60 do change, depending on the latitude.
You will get more practice with this formula in lab.
The Map and Map Projections
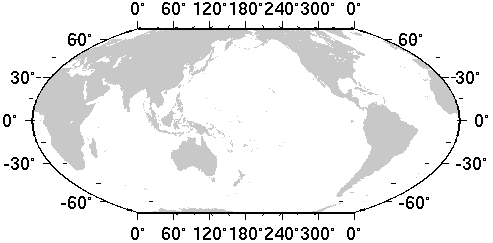
The figures below show the world mapped using 4 different projections. Each projection has certain properties that make it more or less useful for certain applications. Distortions will always occur with projections because we are trying to represent the curved surface of the earth on a flat sheet of paper or flat computer screen. The Mercator projection shown below is one of the most widely used. It has horizontal latitude lines and vertical longitude lines. It is popular for navigational purposes because a line of constant compass direction is always a straight line on this kind of map. However, notice in the Mercator map below that the size of Greenland appears untruthfully large compared with the size of North America! This is because the Mercator projection preserves shape but not area.

Note that in the map above, South latitude is expressed as negative degrees. Also, longitude on this map goees from 0 to 360 degrees. See if you can find Greenland on the Molleweide projection map, next page. Its size in comparison to other land masses is shown much more realistically now. The Molleweide projection preserves area but not necessarily shape.
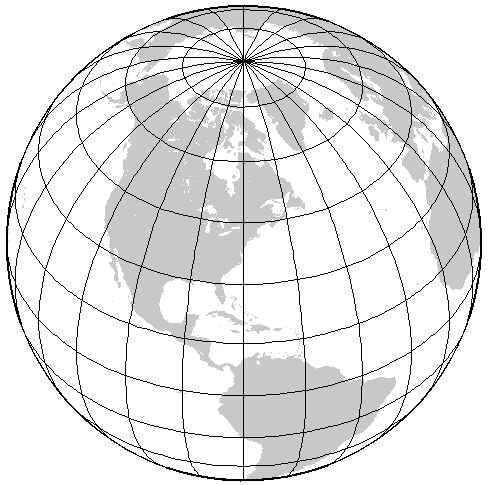
The orthographic projection is yet another way of looking at the world. This type of projection is a perspective view that is often used to give the appearance of the world as seen from outer space. The next page shows an orthographic view of the world centered on North America:
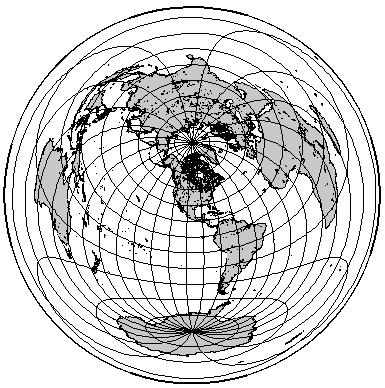
A final example is the azimuthal equidistant projection, which correctly preserves distances on the Earth from at least one or two vantage points. The map on the next pages is an azimuthal equidistant view of the world, centered once again on North America:
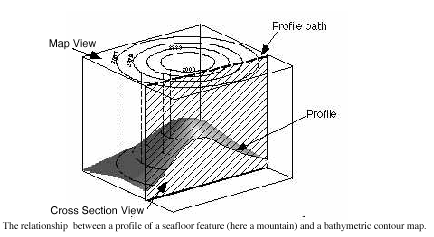
Topographic and Bathymetric Maps
A topographic map records the elevation of terrestrial surface features in distance above mean sea level. A bathymetric map records the depth of submarine earth surface features in distance below mean sea level. Elevation is denoted graphically by contour lines on terrestrial maps. On bathymetric maps these are referred to as either contours or isobaths. Contour lines may be drawn at any interval. If you are a hiker, you are probably already familiar with contour maps.
Bathymetric maps portray the topography of the seafloor. No one really knew what the floor of the deep oceans looked like until SONAR (Sound Navigation Ranging) was invented in 1922 by the U.S. Navy. The system took individual soundings of the ocean floor by recording the amount of time it took for a single sound pulse to reach the bottom and reflect back to hydrophones on the ship's hull. Dr. Harry Hess of Princeton University, as captain of a submarine chaser in the Atlantic during World War II, decided that he could improve the use of SONAR simply by leaving it on, aimed straight downward at the seafloor as the ship moved along. Thus the first ocean floor SONAR profiles were made. We'll talk more about profiles in a second. Other techniques have been developed to record seafloor topography, but SONAR is still the most common. Dr. Dawn Wright of the Geosciences Department uses SONAR to develop extremely detailed maps, images, and profiles of tectonic features on the seafloor. The 3-dimensional image on the next page is of an underwater volcano discovered by Dr. Wright and her colleagues in May of 1996 in the Western Pacific. Go to the class web site to see the image in COLOR and in a much higher resolution. Images such as these are made from advanced seafloor SONAR instruments and have played a critical role in understanding how the seafloor is formed.

Now a profile or transect is a cross-sectional picture of a physical feature plotted on a graph. The figures on the next page (courtesy of Dr. William Prothero, UC-Santa Barbara Geological Sciences) show how this is done. Think of a mountain being sliced from top to bottom by a huge saw. When you look at the structure on one edge, the surface that you see is the profile. In other words, a profile gives you a sideways view of the topography.

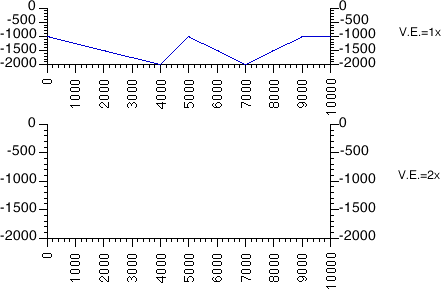
Beware of VERTICAL EXAGGERATION!
Many maps and profiles are produced with vertical exaggeration (V.E.) to help
you see things better, to represent topographic features in greater detail.
V.E. can be very misleading though because if we don't know that it exists for
a map or a profile, we will be led to believe that features are larger than
they really are, which may further lead to faulty interpretations of earth
processes. It is therefore good to be aware of V.E. as a reality check.
Scientists who produce maps or profiles with V.E. should specify the V.E.
somewhere in the map legend or figure caption. V.E. simply means that the
vertical scale is "larger" than the horizontal scale - larger in the sense that
the increment covers the study area in larger detail. The V.E. of a profile is
calculated by dividing the horizontal scale by the vertical scale.
The figure below shows Mt. Hood at V.E.'s of 1, which
is normal (left picture), 2 (center), and 0.5 (right).

Brain teaser: In the figure below, if you completed the profile at a V.E. of 2, how would it compare with the V.E. 1 profile?
The map provided below is a contour map of the ocean floor, contoured in meters below sea level. The map was made from real oceanographic data collected by the National Oceanic and Atmospheric Administration (NOAA). Contours are sometimes omitted where they are very closely bunched (i.e., where the topography is very steep).
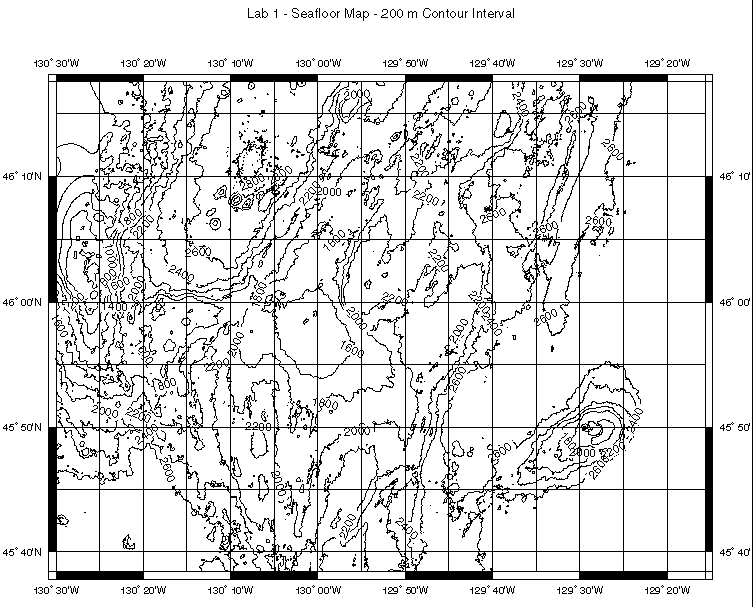
Take some time to
stare at the map a bit and then answer the questions. Download
a separate copy here (postscript format).
(1) In which ocean is this map located? (use a world map)
_____________________________
(2) The region covered by the map is nearest to what coastline? ____________________________
(3) Locate the point 45° 57'N, 130° 00'W. What is the approximate water depth at this location? _______________________. What is the topography like here: fairly steep or flat? How do you know? _______________________________
(4) Locate the point 45° 50'N, 129° 30'W. We'll call this Point A. What is the approximate depth at Point A?__________________________ Is this point a basin, an underwater mountain, or some kind of other feature? __________________________
(5) Locate the point 46° 10'N, 130° 25'W. We'll call this Point B. What is the distance from Point A to Point B in nautical miles? ___________________
(6) Most oceanographic research ships steam along comfortably at 10 knots (i.e., 10 nautical miles/hour). At this rate of speed, how long will it take you to travel from Point A to Point B? _____________________________________
(7) Locate Point C at 45° 50'N, 130° 30'W and Point D at 45° 50'N, 129° 20'W. On the graph provided here or download postscript version), draw a profile (or sideways view) of the ocean floor bathymetry along this line. Note that the horizontal scale is in kilometers and that the vertical scale is in meters. Note also that the vertical scale is in negative meters of depth, which is another way of expressing positive meters below sea level.
(8) On the vertical scale of your profile, determine how many meters is represented by 1 division of the grid. (a) ______________ m
Now on the horizontal scale, determine how many meters is represented by 1 division of the grid. (b) _________________ m (Reminder: 1 km = 1000 m)
Divide (b), the horizontal scale (or distance per unit) on the grid, by (a), the vertical scale on the grid to calculate the vertical exaggeration (V.E.) of your profile. What is the V.E.? _____________________
The map and profile that you have been working with are of a fairly famous
feature called Axial Seamount. Axial Seamount erupted in 1993 AND
1998, thus providing oceanographers with some of the first opportunities to
track an undersea volcanic eruption in near real-time. A color map of the Axial
Seamount region covers the entire surface of Dr. Wright's office door in
Wilkinson Hall, Room 222 on the OSU campus! If you are in the neighborhood, come by
and take a look!
Last update: March 14, 1999
http://dusk.geo.orst.edu/oceans/lab1.html
Dawn Wright & Bob Duncan © 1999